For mathematical definitions see the top-level Addition Chains.
The number of optimal addition chains for n is denoted \(\Lambda(n)\). So for 27 we have \(\Lambda(27) = 5\) since we have 5 different optimal addition chains:
1 2 3 6 9 18 27
1 2 3 6 12 15 27
1 2 3 6 12 24 27
1 2 4 5 9 18 27
1 2 4 8 9 18 27
\(\Lambda\) counts addition chains as unique sequences of numbers without regard to how each element is constructed. For example:
1 2 3 4 7
1 2 3 5 7
1 2 3 6 7
1 2 4 5 7
1 2 4 6 7
\(\Lambda(7) = 5\)
We count only one chain 1 2 3 4 7 even though there are two ways of generating this chain. We have 4 = 3 + 1 and 4 = 2 + 2.
A small table of the early \(\Lambda\) values:
\(n\) \(l(n)\) \(\Lambda(n)\) \(n\) \(l(n)\) \(\Lambda(n)\)
1 0 1 11 5 15
2 1 1 12 4 3
3 2 1 13 5 10
4 2 1 14 5 14
5 3 2 15 5 4
6 3 2 16 4 1
7 4 5 17 5 2
8 3 1 18 5 7
9 4 3 19 6 33
10 4 4 20 5 6
As \(n\) rises we seem to be able to have larger values of \(\Lambda(n)\) presumably because of the combinatorial explosion of being able to rearrange the chains in more ways. Gage Siebert asked if I thought \(\Lambda\) was unbounded. I think the answer is yes based on the following:
We know from [5] that the worst possible addition chain length given by \(l(n)=\lambda(n)+v(n)-1\) (essentially the binary method is optimal) can be attained by integers with their bits spread out enough to precluding adding them in more than one at a time. We can then form the addition chain \(1,2,4,...,2^{\lambda(n)}\). We can continue this chain in \((v(n)-1)!\) ways adding in the remaining bits one by one. For example, for the number 465 we have \(v(465)=5\) so we must have at least \(4!=24\) chains starting \(1,..,2^8\) followed by adding the remaining bits in:
1 10 100 1000 10000 100000 1000000 10000000 100000000 100000001 100010001 101010001 111010001
1 10 100 1000 10000 100000 1000000 10000000 100000000 100000001 100010001 110010001 111010001
1 10 100 1000 10000 100000 1000000 10000000 100000000 100000001 101000001 101010001 111010001
1 10 100 1000 10000 100000 1000000 10000000 100000000 100000001 101000001 111000001 111010001
1 10 100 1000 10000 100000 1000000 10000000 100000000 100000001 110000001 110010001 111010001
1 10 100 1000 10000 100000 1000000 10000000 100000000 100000001 110000001 111000001 111010001
1 10 100 1000 10000 100000 1000000 10000000 100000000 100010000 100010001 101010001 111010001
1 10 100 1000 10000 100000 1000000 10000000 100000000 100010000 100010001 110010001 111010001
1 10 100 1000 10000 100000 1000000 10000000 100000000 100010000 101010000 101010001 111010001
1 10 100 1000 10000 100000 1000000 10000000 100000000 100010000 101010000 111010000 111010001
1 10 100 1000 10000 100000 1000000 10000000 100000000 100010000 110010000 110010001 111010001
1 10 100 1000 10000 100000 1000000 10000000 100000000 100010000 110010000 111010000 111010001
1 10 100 1000 10000 100000 1000000 10000000 100000000 101000000 101000001 101010001 111010001
1 10 100 1000 10000 100000 1000000 10000000 100000000 101000000 101000001 111000001 111010001
1 10 100 1000 10000 100000 1000000 10000000 100000000 101000000 101010000 101010001 111010001
1 10 100 1000 10000 100000 1000000 10000000 100000000 101000000 101010000 111010000 111010001
1 10 100 1000 10000 100000 1000000 10000000 100000000 101000000 111000000 111000001 111010001
1 10 100 1000 10000 100000 1000000 10000000 100000000 101000000 111000000 111010000 111010001
1 10 100 1000 10000 100000 1000000 10000000 100000000 110000000 110000001 110010001 111010001
1 10 100 1000 10000 100000 1000000 10000000 100000000 110000000 110000001 111000001 111010001
1 10 100 1000 10000 100000 1000000 10000000 100000000 110000000 110010000 110010001 111010001
1 10 100 1000 10000 100000 1000000 10000000 100000000 110000000 110010000 111010000 111010001
1 10 100 1000 10000 100000 1000000 10000000 100000000 110000000 111000000 111000001 111010001
1 10 100 1000 10000 100000 1000000 10000000 100000000 110000000 111000000 111010000 111010001
Picking \(n\) with larger values of \(v(n)\) gives unbounded \(\Lambda(n)\) values.
Achim Flammenkamp wrote a program to calculate \(\Lambda\) values by enumerating all addition chains for \(n\) with \(l(n) \le r\). The code built an array of addition chain values keeping track of which values had not been used. If the chain was not at its end position the unused elements were added together and pruned using a class A bound [1] derived from \(c(r)\). \(c(r)\) is the smallest number whose optimal addition chain is of length \(r\). So, \(l(c(r)) = r\) and if \(m < c(r)\) then \(l(m) < r\). A class A bound is very simple. If we are at position \(i < r\) in the chain with an element \(m\) then \(2^{r-i}m\ge c(r)\).
Achim calculated \(\Lambda(n)\) for \(n \le 2^{22}, l(n)\le 22\). I added the class F bounds [2]. To do this we generate the class F bound for each integer \(n\le 2^r\) to calculate the \(\Lambda(n)\) for any \(n\) with \(l(n)\le r\). Since these are lower bounds for element values, we take their minimum value in each position. These bounds halved the search time.
Instead of recursively searching in a depth first manner for addition chains I shifted to a push down stack of problems as described in [1]. This technique though a little more complicated allows the easy conversion of the code to run on multi-core processors. Idle processors/threads can request threads with active values on their stacks to pass the largest problems (the smallest depths) to the idle processors via a queue in global memory. This very nicely scales to even very large core systems.
If you think about how, you might code this search, you need an array of \(l(n)\) values so that you can tell if you find an addition chain for \(n\) at depth \(l(n)=r\). You must record that fact by incrementing the array for the \(\Lambda(n)\) value. Updating \(\Lambda(n)\) requires an interlocked operation as it's done from multiple threads concurrently. These memory accesses and shared memory writes make the code memory bound (limited by the speed of paths to and from memory). We can avoid interlocked operations by splitting the \(\Lambda(n)\) on a per/thread basis and combining at the end of execution.
We waste a lot of time though recalculating stuff. Instead, we should search only for chains of length \(r\) for \(n\) if \(l(n)=r\). So, we run the program with \(r=0\) then \(r=1\) etc. We can dispense with \(l(n)\) values and instead use a bitmap that has a bit set for \(n\) if \(l(n) = r\).
I was running this program on a Dell Precision 7920 Dual Intel 6258R. So, a 58/116 core/thread machine. This machine supports AVX512 and so has registers that can hold 16 32-bit integers. If I restrict the depth to \(r \le 32\) (a huge range) and special case \(n=2^{32}\) I might be able to do even more.
You then meet a problem that seems to be quite well known in the literature [4]. It's hard to use SIMD in backtracking searches since some searches run faster than others and you end up with some slots being unused unless you rebalance. Rebalancing is costly. I got this to work by changing the code that pulls elements from the stack for new problems to actually pull multiple elements if there are gaps and combine them. This seemed to work best if the two problems can be combined to fit into one problem so that one problem can be deleted after combination.
The biggest improvement from AVX512 came from the gathered read. If you imagine at depth \(r\) we have up to 16 integers packed into a zmm register. We want to look each value up in a bitmap and only if the bitmap is set increment the \(\Lambda\) array. I use the _mm512_mask_i32gather_epi32 intrinsic to read from the bitmap in parallel. Each \(n\) is shifted down by 5 bits to create a 32-bit element offset in the bitmap. Anding the \(n\) with 31 give the bit number. The gather loaded values are shifted down by the bit number and only the values that had the bottom bit set are used to increment the \(\Lambda\) values.
It turns out that much to my surprise the code spends much of its time finding non-optimal chains so rejecting in parallel is a big deal. So, there must be way more no-optimal chains of length \(r\) than optimal ones. With this code I was able to generate \(\Lambda(n)\) for \(n\le 2^{28},l(n)\le 28\). Starting with the generation 4 EPYC processors AMD started to support AVX512. So, I built a machine with dual 9654 EPYC processors. Thats 96 (cores) * 2 (sockets) * 2 (threads) * 16 (32 bit integer slots) = 5888 concurrent searches. In under a week this allowed me to calculate all \(\Lambda(n)\) for \(n\le 2^{29},l(n)\le 29\). To address somewhat the issue of the large number of non-optimal chains I added code to record as a bitmask if each chain element has been used. Achim had a similar prune in his code, and I used it in my 2010 paper. Obviously, we have to maintain 16 such bitmasks. The data can be downloaded here:
The code can be found here:
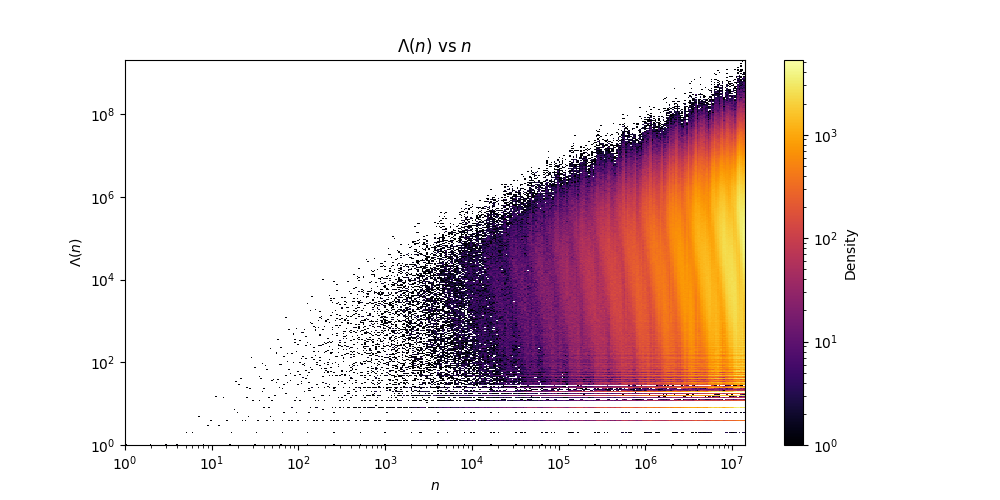
The text file format is the same as the tables shown above. \(n\) followed by \(l(n)\) and then by \(\Lambda(n)\). Note that the file is sparce since it contains no numbers \(n\) with \(l(n)>29\). The file should be dense up until \(c(30)=14143037\), since this is the first number requiring more than 29 steps in its optimal addition chains. Gage Siebert kindly sent me python code to generate this fascinating heat map of \(\Lambda(n)\) against \(n\):

Knuth [3] says that for \(c(r)\) values "The computation of \(l(n)\) seems to be hardest for this sequence of n's". This leads some authors to think that finding optimal chains for \(c(r)\) values is hard. In fact, this is not the case. If you know \(l(c(r))\) then finding chains appears to be easy as they have very large numbers of chains. What is hard is proving that there is no chain shorter than \(l(c(r))\). Do the \(c(r)\) values have the largest number of chains for all numbers with \(l(n)=r\)? We might think this is true since a chain for \(c(r)\) may contain any number \(m<c(r)\) since \(l(m)<r\).
We explore this question in the following table. \(\Lambda^m(r)\) is the number \(n\) with \(l(n)=r\) with the largest \(\Lambda(n)\) value. Values may tie and, in that case, we show them all.
| \(r\) | \(c(r)\) | \(\Lambda(c(r))\) | \(\Lambda^m(r)\) | \(\Lambda(\Lambda^m(r))\) | \(r\) | \(c(r)\) | \(\Lambda(c(r))\) | \(\Lambda^m(r)\) | \(\Lambda(\Lambda^m(r))\) | \(r\) | \(c(r)\) | \(\Lambda(c(r))\) | \(\Lambda^m(r)\) | \(\Lambda(\Lambda^m(r))\) |
| 0 | 1 | 1 | 1 | 1 | 11 | 191 | 9787 | 191 | 9787 | 22 | 110591 | 1517938 | 155604 | 29390402 |
| 1 | 2 | 1 | 2 | 1 | 12 | 379 | 9076 | 508 | 17961 | 23 | 196591 | 6556097 | 311208 | 55506704 |
| 2 | 3 | 1 | 3,4 | 1 | 13 | 607 | 31373 | 758 | 33076 | 24 | 357887 | 2973869 | 551880 | 97132092 |
| 3 | 5 | 2 | 5,6 | 2 | 14 | 1087 | 55262 | 1214 | 110624 | 25 | 685951 | 13736135 | 1103760 | 208839226 |
| 4 | 7 | 5 | 7 | 5 | 15 | 1903 | 68810 | 2540 | 230110 | 26 | 1176431 | 10619809 | 2207520 | 406164668 |
| 5 | 11 | 15 | 11 | 15 | 16 | 3583 | 57443 | 5080 | 413376 | 27 | 2211837 | 7266410 | 4415040 | 732644565 |
| 6 | 19 | 33 | 22 | 40 | 17 | 6271 | 209898 | 8436 | 780274 | 28 | 4169527 | 15095632 | 7257602 | 2032609296 |
| 7 | 29 | 132 | 29 | 132 | 18 | 11231 | 252024 | 16872 | 1508603 | 29 | 7624319 | 13052461 | 14515204 | 3890516904 |
| 8 | 47 | 220 | 58 | 352 | 19 | 18287 | 665583 | 33744 | 2533736 | |||||
| 9 | 71 | 1258 | 71 | 1258 | 20 | 34303 | 1158949 | 48482 | 5110044 | |||||
| 10 | 127 | 2661 | 142 | 3903 | 21 | 65131 | 1661908 | 77802 | 12383931 |
As a byproduct of some other work, I calculated \(\Lambda(2^n-1)\) so I thought I should record them here:
| \(n\) | \(\Lambda(2^n-1)\) | \(n\) | \(\Lambda(2^n-1)\) | \(n\) | \(\Lambda(2^n-1)\) | \(n\) | \(\Lambda(2^n-1)\) | \(n\) | \(\Lambda(2^n-1)\) | \(n\) | \(\Lambda(2^n-1)\) | \(n\) | \(\Lambda(2^n-1)\) |
| 1 | 1 | 11 | 62061 | 21 | 868351 | 31 | 15952501 | 41 | 5463728 | 51 | 2122768 | 61 | ? |
| 2 | 1 | 12 | 824 | 22 | 937383 | 32 | 1920 | 42 | 34388888 | 52 | 9720984 | 62 | ? |
| 3 | 5 | 13 | 24329 | 23 | 24266 | 33 | 53712 | 43 | 277076 | 53 | 570029243 | 63 | ? |
| 4 | 4 | 14 | 45448 | 24 | 10656 | 34 | 81376 | 44 | 17390164 | 54 | 9944052 | 64 | 23040 |
| 5 | 77 | 15 | 11506 | 25 | 377250 | 35 | 16409576 | 45 | 6655234 | 55 | 858773497 | ||
| 6 | 87 | 16 | 192 | 26 | 507044 | 36 | 393608 | 46 | 363176 | 56 | 14733116 | ||
| 7 | 2661 | 17 | 4432 | 27 | 198950 | 37 | 12648428 | 47 | 306156569 | 57 | 992431328 | ||
| 8 | 24 | 18 | 18708 | 28 | 606346 | 38 | 24412815 | 48 | 178368 | 58 | ? | ||
| 9 | 944 | 19 | 860201 | 29 | 31008359 | 39 | 9211094 | 49 | 5597296 | 59 | ? | ||
| 10 | 1072 | 20 | 11280 | 30 | 404996 | 40 | 190176 | 50 | 13502390 | 60 | 13713216 | 128 | 322560 |
The entries marked with '?' would require 8 small steps and I haven't let any of them run to completion.
The addition chains for \(2^{2^n}-1\) appear to be quite constrained with their non-doubling steps having no carries. This led me to think that there might be a simple formula for their \(\Lambda\) values.
We can make the conjecture that \(\Lambda(2^{2^n}-1)=2^{n-1} n!, n>0\) as given by this sequence A002866 - OEIS
[1] Thurber EG (1999), "Efficient Generation of Minimal Length Addition Chains", SIAM Journal on Computing. Vol. 28(4), pp. 1247-1263.
[2] Thurber EG and Clift NM, "Addition chains, vector chains, and efficient computation", Discrete Mathematics, Volume 344, Issue 2, 2021,
[3] Knuth DE (1998), "The art of computer programming, 2: seminumerical algorithms, Addison Wesley", Reading, MA. , pp. 477
[4] Powley, Curt, Chris Ferguson, and Richard E. Korf. "Depth-first heuristic search on a SIMD machine." Artificial Intelligence 60.2 (1993): 199-242.
[5] Hansen, W. Untersuchungen über die Scholz-Brauerschen Additionsketten und deren Verallgemeinerung 1957 Göttingen